Written for Computational Culture (forthcoming, #9, preprint with permission). Official Version.
Written for Computational Culture (forthcoming, #9, preprint with permission). Official Version.
Review of Joque, Justin. Revolutionary Mathematics: Artificial Intelligence, Statistics and the Logic of Capitalism. London and New York: Verso, 2022.
Datafication has been the hallmark of modern governance, all the way back to the definition of statistics as “science of data about the state” in mid-18th century Prussia. Creating reductionist regularity, abstracting from the infinite complexity of local, embodied experience, enabled a new scale and complexity by which the state could organize the life of its subjects, in pursuit of variable political agendas. In the mid-19th century, the philosopher Auguste Comte (1798-1857) introduced a hierarchy of the sciences, with physics at the top for its mathematics-enabled generality, setting off mathematics envy in the social sciences (which he placed at the bottom of the ladder). This was most consequential in economics, but its reverberations are still felt in the recent creation of the “digital humanities”, quantifying the remaining, previously staunchly qualitative fields of knowledge. At the end of the 19th century, rapidly growing corporations, encountering their own need to extend the scale and complexity of governance practices, also turned to large-scale datafication (and automated data processing) to stave off the impending “control crisis” [1].
A new type of quantified knowledge
Given this long line of quantification at the heart of governance and knowledge production, there is now considerable debate over the degree to which the most recent wave of quantification, “big data”, constitutes a historical continuation or a historical break [2]. In his new book “Revolutionary mathematics” Justin Joque comes down in the second camp by locating this break very precisely: the shift in the main statistical methods used to turn data into knowledge and the types of truth claims these produce, a shift from “frequentist” to “Bayesian” statistics. Joque’s interest is less in the technical and mathematical dimensions of this shift, but in the political, epistemological and metaphysical consequences and the dynamics of subjectivation they produce.
In the following, I will first summarize, quite freely, the main argument of the book and then try to assess it. The first part will take a bit longer than usual, because basic mechanics of Bayesian statistics are that not easy to grasp, even though Joque makes a much better job at explaining it than much of the technical literature out there.
While Bayesian statistics takes its name from Thomas Bayes (1702 – 1761), an English mathematician and Presbyterian minister, much of 19th and 20th-century statistics was resolutely frequentist. This is the kind of statistics most non-mathematicians know, focused on averages and fixed probabilities extracted from large, uniform data sets. Think of distributions of height in populations, or the probability of a repeatable event, such as a coin toss. Joque highlights three features of probabilistic knowledge produced by frequentism. First, probability is known only after the fact, at the end of a long series of repetitive measures, of, say, 10,000 coin tosses or 10,000 army recruits. Second, frequentist statistics work on a group level and cannot be applied to single events. To the degree that it makes sense to say a single coin toss has a 0.5 probability to come up with heads, it’s only because it's part of a class of events, coin tosses, in which they overall probability has already been established. Third, frequentist probability is fixed and objective. It represents “the long-run frequency of a physical system” (113). In its ideal version, it does not change over time or with additional data, and it provides accurate knowledge about real world events.
But there is a catch. “Unlike nonstatistical forms of knowledge, statistical analyses always face the possibility that what was observed, at officially significant levels, was merely the result of random chance” (115). Initially, this was not a problem. 18th century mathematicians (many of them, like Bayes, priests) assumed that it was god that spoke through the regularity revealed in statistics. This, in itself, was a new assumption, because medieval epistemology assumed that god would speak through irregularities (a calf born with two heads, a freak storm etc). In media theory terms, which Joque does not use, one could say this new focus on regularity expressed key features of print culture and suited the needs of the emerging systems of state power and later industrial managerialism. As theological commitments waned, an approach was needed to mitigate the risk of frequencies revealing chance, rather than objective regularities. In 1925, Ronald Fisher (1890-1962), one of the founding figures of 20th century statistics (and staunch eugenist and racist [3]), introduced the notion of the p-value, that is, the probability that a statistical measure is the result of a chance operation, rather than of actual regularities. Any p-value higher than 5%, he argued, should be taken to mean that the result is statistically insignificant. Today, the meaning of the p-value has changed in subtle but significant ways. What used to be a measure for falsification, the p-value providing a threshold of certainty for insignificance, turned into a measure of verification. Any p-value below 5% is taken to represent an actual regularity and hence a scientifically valid result. Publication pressures in the sciences have led to a practice called “p-hacking” meaning the manipulation of statistical techniques in order to create a p-value smaller than 5%, undermining the key promise of frequentism as objective measure of physical regularities.
Bayesian statistics, on the other hand, makes very different claims about the world. Rather than indicating the probability of an event taking place, it calculates the likelihood of a hypothesis about the event being true, given another event one observes. In other words, probability is no longer understood as the actual frequency of some repetitive phenomenon, rather, it is interpreted as reasonable expectation, representing a state of knowledge, or quantification of a personal belief.
The basic formulation of Bayes Theorem, independently discovered and formalized by the French polymath Pierre-Simon Laplace (1749 - 1827) is quite simple in mathematical term, but, as Joque argues convincingly, profound in its epistemological consequences:
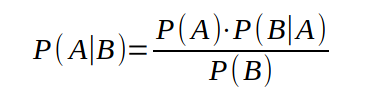
Predicting a singular event
Let’s assume we are TV journalists covering the night of a general election. Our hypothesis is: candidate X will win over candidate Y. We don’t want to simply wait for the final result to be announced, but want to be, say, 90% certain about the hypothesis being true (or false) so that we can call the election on TV before the final results are in. A frequentist approach cannot work here, because an election is a singular event. But a Bayesian approach can. P(A|B) is the probability (P) of our hypothesis (A) being true, given what we just observed (B). This is called the “posterior probability”. This is the number we want to know and we are satisfied once it has reached 90%.
Now the results from the districts (B1-n) are slowly coming in and the calculation starts. The first number needed is the “prior probability” P(A). This is what we already know before the new observation. At the start, it’s an (educated) guess, or a belief, about the likelihood of X winning over Y, hence our hypothesis being true. Since no results are in yet and all we know is that there are two candidates, a good guess would be that the probability of X winning is 50%. The next number needed is called the “likelihood” P(B|A): the probability of the event occurring if the hypothesis is true. If candidate X wins the overall election, how likely is he to win this particular precinct (Bx)? And the last number we need to know is called the “marginal” P(B), that is the probability of candidate X winning Bx independent of the outcome of the overall election. The likelihood and the marginal for each precinct are calculated in advance, based on previous elections.
Now, Candidate X has won the first precinct B1 and we plug the prior probability, the likelihood for B1, and the marginal for B1 into the formula. As a result, we get the first posterior probability of, say, 55%. Not very good, but better than the 50% we started with. Then the result of the next precinct, B2, comes in. The just calculated posterior probability becomes our new prior probability, we add the likelihood for B2 and the marginal for B2 and calculate again. Maybe candidate Y won this one, but if this precinct is a “safe one”, meaning the party of candidate Y has always won it, even when it lost an overall election, the probability of the hypothesis being true has not changed, it still stands at 55%. With each result from a new precinct, the same calculation is repeated until we reach desired probability of 90% (or, inversely, 10%). Then we can go on TV and announce the winner.
For much of the 20th century, this mode of calculating probabilities remained deeply unpopular for philosophical, epistemological and practical reasons. Philosophically, the use of the prior – a number seemingly plucked from thin air, an educated guess, a subjective belief – was abhorred by academic statisticians craving objectivity. Joque covers their repulsion in vivid detail. Epistemologically, the results calculated are unstable, they can change with every new observation and provide local, subjective, rather than universal objective knowledge. Again, this was viewed as very unscientific. And, finally, the computational complexity, or at least the tedium of having to do the same calculations over and over again, escalates very quickly making the approach unpractical as long as the computation had to be done by humans.
Now, computers have largely overcome the practical limitations. More importantly, for the financial industry, or financialized capitalism more generally, the features abhorred by frequentist statisticians for theoretical and epistemological reasons, are the very things which are most valuable from a business perspective. The financial trader has no interest in universal truth, the system is too large and too dynamic to ever obtain this. What she is interested in is risk management, that is, the quantification of (un)certainty under the conditions of incomplete and constantly changing information. Under these circumstances, what is truth? Put simply, acceptable risk. And what is acceptable risk? A situated, financial calculation where the possible gain from an action (if the hypothesis turns out to be right), is larger than its possible loss (if the hypothesis turns out to be wrong). In other words, truth and profit become the same.
Truth as risk
Let’s go back to election night. The journalists need to set a threshold by which they accept their hypothesis as true. 90% in our example. How does this number come about? It’s not a fixed number like the p-value, which is the same for everyone across all contexts. On the contrary, it’s the result of a subjective risk/reward calculation. The reward is the attention and the reputation to be gained from being the first TV station to call the election correctly. The risk is the reputational damage that comes from going out too early and calling the election wrongly. Thus the threshold of 90% is a subjective one, based on a situated calculation of profit and loss. A more serious TV station might set it higher, a less serious one lower.
This is not entirely new. Bayesian statistics, while academically marginalized and practically cumbersome until very recently, have been applied in the insurance industry since at least the mid-20th century, as Joque shows, because they are effective for managing risk, no matter that theoretical statisticians balked at its epistemic foundation. The first election to be covered on TV in this manner was, as Jill Lepore [4] recounts in fantastical detail, the US presidential election of 1952. However, even accounting for the increased overall importance of the financial industry, which relates to the world in predominantly Bayesian terms, until quite recently one might have still been able to argue that the influence of Bayesian thinking is limited to a specific, though very powerful, sector.
However, this is no longer the case. The machine learning (ML) revolution in artificial intelligence has spread Bayesian approaches into all corners of our culture, indeed, as Joque argues, it has become hegemonic, providing nothing less than “the statistical theory of the information age” (151). There are several features that makes this type of calculation so relevant to implementation in ML. First, it can be automated to feed back on itself. Second, it is suited to single events allowing for endless dividuation of cases and subjects. Third, it can start from a position of non-knowledge. In ML, variables are often deliberately set randomly at the beginning of the learning process, in order to avoid “bias”. Though, as is well known now, this is a far too narrow understanding of bias to actually get rid of it [5]. Finally, it calculates a situated relation – the probability of a hypothesis advanced by the learning subject (which can be a machine) about the calculated object (which can be a human being) being true. Bayesian classifiers used in image recognition software create knowledge such as a person being “40% happy”, meaning there is a 40% change that a particular facial expression correlates with happiness. Whether or not we accept this as “true”, meaning reliably enough to act upon, depends on the threshold we set, which depends on the cost/benefit calculation underlying the particular operation. If the task to be decided is which advertisement to show, then a 40% certainty is often enough to trigger the happy add.
Epistemology of speculation
Bayesian truth – this is one of Joque’s main points – is very different from the stable, universalist claims advanced by scientific epistemology that defined modernity (and frequentist statistics). Truth here is local and highly dynamic, it can, and should, change all the time, as new (objective) information comes in, or as the (subjective) hypothesis or risk/reward calculation changes. It’s a type of truth that allows to calculate the risk of one-time, on the spot exchanges in the market, rather than gain reliable knowledge about the world. Such “a model is never universal but always a particular and local abstraction. Machine learning appears to establish precisely what capitalism has always dreamed of: a smooth, universal lingua franca of epistemic and economic commensurability that always produces its truth only at the exact local moment of exchange” (169). Once the exchange has taken place, that knowledge is discarded or, more precisely, becomes just one of a myriad of variables in the calculation of the next hyper-local truth. And because the truth is so local and short-term, addressing just the next exchange, the difference between correlation and causation becomes practically irrelevant. The occasional (or even frequent) mistakes this generates are just part of the risk calculation and not a bug in the system. It can also never be fully falsified. Even a 99% certainty that it will rain tomorrow includes at the same time the possibility of it not doing so.
This, Joque argues, has profound consequences, because this type of epistemology creates knowledge suited primarily for short-term risk/reward calculations. As he points out, all
statistical models provide mathematical abstractions of the world; they take a varied and disparate world and reduce it to data that is then further reduced to a model that can extrapolate to new data. Yet unlike traditional Western thinking around abstractions, these models are not indexical of any stable world outside the constant flux of the data they ingest. The statistical abstractions that functionally underwrite the discoveries of machine learning rediscover their index in the fluidity of exchange, a foundation that does not point elsewhere to some transcendent ideal but rather immanently to the reasoned exchange of contracts and bets. (166)
This type of self-referential fluidity permeates all those aspects of life that are either financialized or shaped by machine learning, which is increasingly every aspect of life. For most people, this is felt only indirectly, as an experience of living in a world that is increasingly nonsensical, because the way the world and they themselves are calculated, automatically treated and, sometimes, directly addressed, is incommensurate with the type of modern, coherent subject they imagine themselves to be. But to others, this opens the path to a new system of belief. Just listen to the tech bros on YouTube who breathlessly explain how Bayesian thinking help them to constantly improve all aspects of their lives. If that wasn’t cheesy enough, quite a few of these videos are shot on top of hills or mountains.
For Joque, “it is a world without the traditional subject precisely because, in algorithmic form, the distinction between subject and object evaporates; one must act in accordance with what the algorithm will calculate about them, like a content producer constantly trying to optimize their search engine ranking. Each looks more and more like the other, and both subject and object become free, in a way, but only to follow the laws of the system” (170).
Given the scale of epistemic shift and the breadths of its consequences to everything from truth claims to subjectivation the reader might assume that Bayesian statistics is the revolutionary mathematics that Joque alludes to in the title of the book. But it isn’t. His goal is to go further and to think about ways of overcoming the logic of exchange and profit that shape contemporary financialized and automated reasoning.
What is clear to Joque is that
we cannot seek a return to some natural, pretechnological, prestatistical, precapitalist form. Nor can we take seriously the resolute position of the liberal subject—of one who can know, and functionally audit, the complexity of these algorithmic systems so as to solve these problems through reform alone. … Instead, we must transform the necessity of what is already conventional and structurally fluent within the statistically ordained world: abstraction in all its alienatory power. To abolish capitalism, what is needed is, rather, a full embrace of the forces of alienation, especially as they are created through machines that automate and extend humanity’s ability to produce and think. … Rather than attempt to construct an impossible, unalienated form of capitalism, we must free alienation from capitalism. (186-190).
Under conditions of climate change, planetary infrastructures, and multi-species sensing, the modern subject is no longer a productive foundation for emancipatory projects, rather abstraction and alienation from immediate experience are a necessary part of the contemporary.
Freeing alienation from capitalism
Up to here, it’s easy to follow Joque. Beyond this, things get, not surprisingly, quite vague. What that means for mathematics, what a revolutionary mathematics would require, what it’s relation to machine learning and other forms of situated knowing might be, remains quite unclear. While this is an impossibly large question, some perspectives to begin addressing it do exist. The quite substantial literature on the epistemology of the financial markets, be that in its more popular [6] or more philosophical articulation [7] might be a good starting point. Taleb in particular is quite clear that the established risk/reward calculations have very significant short-comings when it comes to rare but high-impact events (black swans). This point to the understanding, even within perspectives affirmative of financialization, of the internal contradictions, or at least practical limitations, of Bayesian epistemology. In terms of Bayesian ML, if truth is a risk/reward calculation, then one could think about changing these parameters by increasing the costs of getting it wrong. At the moment, misclassification is a frequent occurrence in ML system because the downside risks for the actors doing the classification are so extremely low. Showing someone the wrong ad has, essentially, no cost, so a lot of risk can be accepted (this is why we all see so many personalized but still seemingly random ads). The same is true when sorting job applications. For the employer the risk of missing a few qualified applicants is worth the costs of streamlining the HR process (which wasn’t perfect to begin with anyway). For the job seeker being denied an interview again and again, the costs might be very high. However, they play no role in the risk/reward calculation embedded in the screening software. Current EU regulation, which includes a right to explanation, is aiming to change the risk calculation in favour of the calculated.
This lack of imagination about how to address the problems stated might also be a consequence of focussing the history of statistics almost exclusively on the history of academic debates. In this way, Joque loses some of the historical complexity of the interplay within the “motley conglomerate of game theory, nuclear strategy, operations research, Bayesian decision theory, systems analysis, rational choice theory, and experimental social psychology” that characterized cold war planning [8]. In many fields which had to address the probability of one-time events, such as a nuclear war, the division between frequentist and Bayesian approaches was much less clear cut then in the academic debates Joque covers. Rather, methods were mixed and some of the questions that are today addressed by Bayesian approaches were addressed indirectly by non-Bayesian means. Of course, this more historical view lends itself less to arguing for a hard historical break.
However, what might be a historical simplification brings conceptual clarity without overly distorting the record. All in all, Joque’s book is groundbreaking. It’s the first comprehensive treatment of the epistemic, philosophical, and political dimensions of the growing significance of Bayesian statistics (popular accounts such as McGrayne’s [9] don’t even come close). He does succeed in showing how closely aligned the epistemic foundations of financialized capitalism and contemporary artificial intelligence really are. This is no mean feat and is eye-opening. To break this alignment, to rethink risk/reward calculations beyond the financial and truth beyond the price without reverting to transcendental universalism is a task as necessary as it is daunting. And Joque’s book is an important contribution to this collective endeavour.
Notes:
[1] Beniger, James R. The Control Revolution: Technological and Economic Origins of the Information Society. Cambridge, MA: Harvard University Press, 1986.
[2] Koopman, Colin. How We Became Our Data: A Genealogy of the Informational Person. Chicago: The University of Chicago Press, 2019.
[3] Southern Poverty Law Center. “Garrett Hardin.” Southern Poverty Law Center, n.d. https://www.splcenter.org/fighting-hate/extremist-files/individual/garrett-hardin (last accessed: 21.07.2022)
[4] Lepore, Jill. If Then: How One Data Company Invented the Future. London: John Murray (Publishers), 2021.
[5] O’Neil, Cathy. Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy. London: Allen Lane, Penguin Random House, 2016; Benjamin, Ruha. “Assessing Risk, Automating Racism.” Science 366, no. 6464 (October 25, 2019): 421–22.
[6] Taleb, Nassim Nicholas. The Black Swan: The Impact of the Highly Improbable. Random House trade paperback edition. New York: Random House, 2008.
[7] Ayache, Elie. The Medium of Contingency: An Inverse View of the Market. Houndmills, Basingstoke, Hampshire ; New York, NY: Palgrave Macmillan, 2015.
[8] Erickson, Paul, Judy L. Klein, Lorraine Daston, Rebecca M. Lemov, Thomas Sturm, and Michael D. Gordin. How Reason Almost Lost Its Mind: The Strange Career of Cold War Rationality. Chicago ; London: The University of Chicago Press, 2013, p.4.
[9] McGrayne, Sharon Bertsch. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted down Russian Submarines, & Emerged Triumphant from Two Centuries of Controversy. New Haven [Conn.]: Yale University Press, 2011.